My Erdös Number is Five

1 2 3 4 5 6 7 8

Who was Paul Erdös?

Back to Top

Mathematicians in general have fewer links and lower numbers. But physicists can play too! If you are an experimentalist, the approach is to link first to a theorist, and thence to a mathematician. It can get very tricky. On my first attempt, I built an extremely convoluted path that yielded a number of 8, starting with my colleague Pierre Extermann:

(1.) J. Marasco/P. Extermann 1971

(2.) P. Extermann/W. Haeberli 1965

(3.) W. Haeberli/H. H. Barschall 1971

(4.) H. H. Barschall/J. A. Wheeler 1940 (!!!)

Sometimes to go forward, you must first go backward. This is the experimentalist-to-theorist crossover in this chain.

(5.) J. A. Wheeler/R. P. Feynman 1945, 1949

I was delighted that my chain went through Feynman. Poetic justice! Note that Feynman has an Erdös Number of 3.

(6.) R. P. Feynman/N. Metropolis 1949

(7.) N. Metropolis/S. Ulam 1951, 1953, 1955

(8.) S. Ulam/P. Erdös 1979

With some additional research using Google Scholar, I was able to reduce this to 5. We traded Feynman for Ypsilantis, and shorted the path by three links.

Here is the documentation trail of the links. Ronald Mermod (one of my two thesis advisors) and Tom Ypsilantis are/were experimental physicists. Nicholas ("Nick") Metropolis was generalist who did some of the earliest work on the Monte Carlo method; today you would call him a mathematical physicist. He is the crossover to the world of the mathematicians. From there it is two brief steps via Stanislauw ("Stan") Ulam, who was also very definitely a generalist with eclectic tastes.

For the curious, my other thesis advisor was René Turlay, who collaborated with Fitch and Cronin in the discovery of CP-violation in K-meson decays. Even though Fitch and Cronin later won the Nobel Prize, I could not link to Erdös through them. I also tried Pierre Piroué, but that didn't help either. Nor did Paul Kunz.

1 2 3 4 5 6 7 8

Erdös has a Marasco Number of 5

Back to Top

1 2 3 4 5 6 7 8

Link 1:

 Marasco and Mermod

Back to Top

These were the first two papers I ever published, working in the University of Geneva/Saclay collaboration at CERN in the late sixties and early seventies, led by Ronald Mermod (Switzerland) and René Turlay (France):

Physics Letters B

Volume 36, Issue 6, Pages 541-636 (18 October 1971)

Measurement of K_e4⁺ - decay rates and test of the ΔS = ΔQ rule 
Pages 615-618
M. Bourquin, J. P. Boymond, P. Extermann, J. Marasco, R. Mermod, P. A. Piroué and H. Suter P. Basile, S. Brehin, A. Diamant-Berger, P. Kunz, M. Lemoine et al.

Determination of the low-energy − phase shifts and form factors in K_e4⁺ decay 
Pages 619-622
P. Basile, S. Brehin, A. Diamant-Berger, P. Kunz, M. Lemoine, R. Turlay and A. Zylbersztejn M. Bourquin, J. P. Boymond, P. Extermann, J. Marasco, R. Mermod et al.

For a full list of my publications, click here.

The first Greek, Ypsilantis, gets into the act!

Phys. Rev. 108, 1553–1556 (1957)

Issue 6 – 15 December 1957

Experiments on Antiprotons: Antiproton-Nucleon Cross Sections

O. Chamberlain, D. V. Keller, R. Mermod, E. Segrè, H. M. Steiner, and T. Ypsilantis
Radiation Laboratory and Department of Physics, University of California, Berkeley, California

1 2 3 4 5 6 7 8

Link 2:

 Mermod and Ypsilantis

Back to Top

1 2 3 4 5 6 7 8

Link 3:

 Ypsilantis and Metropolis

Back to Top

Metropolis provides even more Greek influence. But, hey, that's where Superman lived!

Phys. Rev. 105, 302–310 (1957)

Issue 1 – 1 January 1957

Phase-Shift Analysis of 310-Mev Proton-Proton Scattering Experiments

H. P. Stapp and T. J. Ypsilantis
Radiation Laboratory and Department of Physics, University of California, Berkeley, California

N. Metropolis
Los Alamos Scientific Laboratory, Los Alamos, New Mexico

Ulam was Polish-American. Nick and Stan published three times together. Here are the citations from Google Scholar:

[CITATION] The Monte Carlo method
S Ulam, N Metropolis - Journal of American Statistical Association, 1949
Cited by 10 - Web Search

In an amazing coincidence, this article was used by me in 1966 as the basis for a Monte Carlo simulation performed on an IBM 1620 for a senior thesis in Chemical Engineering at The Cooper Union. Another paper, also co-authored by Metropolis, was also instrumental. The resulting paper placed second in a regional AIChE contest, but was never published.

[CITATION] A Property of Randomness of an Arithmetical Function
N Metropolis, S Ulam - American Mathematical Monthly, 1953
Cited by 3 - Web Search

[CITATION] On certain sequences of integers defined by sieves
V Gardiner, R Lazarus, M METROPOLIS, S ULAM - Math. Mag, 1955
Cited by 3 - Web Search

1 2 3 4 5 6 7 8

Link 4:

 Metropolis and Ulam

Back to Top

1 2 3 4 5 6 7 8

Link 5:

 Ulam and Erdös

Back to Top

Ulam and Erdös were great friends, and the Erdös Number site claims they published jointly 3 times. Below is the only citation I could find. I've always wondered what language they spoke when they collaborated. Here is the final link in the chain:

Minimal decompositions of two graphs into pairwise isomorphic subgraphs

Proceedings of the 10th Southeastern Conf. on Comb., Graph Theory and Computing (1979), 3-18

F.R.K. Chung,  P. Erdös, R. L. Graham, S. M. Ulam and F. F. Yao

[CITATION] Minimal decompositions of two graphs into pairwise isomorphic subgraphs
FRK Chung, P Erdös, RL Graham, SM Ulam, FF Yao - Proceedings of the Tenth Southeastern Conference on …
Cited by 2 - Web Search

Just to show what a small world this is, Chung and Graham did the graph theory solution of the Stomachion problem in 2003, a problem with which I had a certain involvement.

"According to Erdös Number Facts, approximately 268,000 people are known to have finite Erdös numbers. Among these, 5 is both the median (value with the closest to equal numbers above and below) and the mode (most common value), with 87,760 people having number 5. Here are some well-known names with Erdös number 5 from Some Famous People with Finite Erdös Numbers.

• Luis W. Alvarez
• John Bardeen
• Niels Bohr
• Louis de Broglie
• Francis Crick
• George Gamow
• Alexander Grothendieck
• Tsung-dao Lee
• Paul A. Samuelson
• Arthur L. Schawlow
• Glenn T. Seaborg
• Arnold Sommerfeld
• Alan Turing

Note that in most cases Erdös numbers are an upper bound. Particularly for people with higher numbers, there's always the possibility an obscure publication or unexplored path will reduce their numbers. An individual's number may decrease if any of the authors in their path publishes a paper with anybody whose number is less than their previous predecessor, or if a new shorter path is created when an individual's Erdös number is reduced."

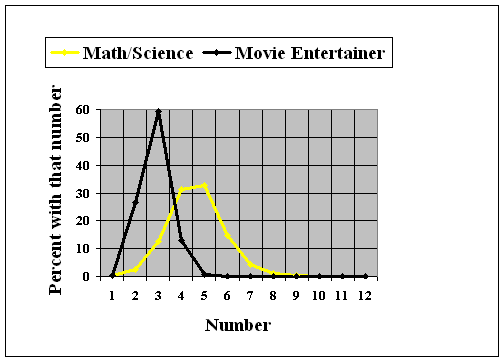
It is somewhat interesting to compare Erdös Numbers to Bacon Numbers. In the latter case, low numbers are quite common, and the game consists of finding obscure people with high numbers. In the former, the objective is to minimize your number. A comparison of the two distributions is revealing:

        0  ---         1 person
        1  ---     504 people (0.18%)
        2  ---    6,593 people (2.5%)
        3  ---  33,605 people (12.6%)
        4  ---  83,642 people (31.2%)
        5  ---  87,760 people (32.7%)
        6  ---  40,014 people (14.9%)
        7  ---  11,591 people (4.3%)
        8  ---   3,146 people (1.2%)
        9  ---     819 people (0.31%)
       10  ---    244 people (0.09%)
       11  ---     68 people (0.02%)
       12  ---     23 people (0.009%)
       13  ---      5 people (0.002%)

1 2 3 4 5 6 7 8

More about Erdös Numbers

Back to Top

Back to Top

Click here to e-mail Barbecue Joe on the subject of Erdös Numbers

Back to Barbecue Joe